How to Calculate and Solve for the Radius, Height and Surface Area of a Spherical Segment | The Calculator Encyclopedia

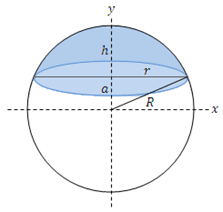
The image above is a spherical segment. To calculate the surface area of a spherical segment requires two essential parameters which are the radius of the sphere (R) and the height (h).

The formula for calculating the surface area of the spherical segment:

A = 2πRh

Where;
A = Surface area of the spherical segment
R = Radius of the sphere
h = Height of the spherical segment

Let’s solve an example;
Find the surface area of a spherical segment when the radius of the sphere is 12 cm and the height is 16 cm.

This implies that;
R = Radius of the sphere = 12 cm
h = Height of the spherical segment = 16 cm

A = 2πRh
A = 2π (12 x 16)
Then, A = 2π (192)
A = 6.28 (192)
A = 1206.37

Therefore, the surface area of the spherical segment is 1206.37 cm².

Calculating the Radius of the Sphere using the Surface Area of the Spherical Segment and the Height

R = ^A / _2πh

Where;
R = Radius of the sphere
A = Surface area of the spherical segment
h = Height of the spherical segment

Let’s solve an example;
Find the radius of a sphere with a surface area of 300 cm² and a height of 12 cm.

This implies that;
A = Surface area of the spherical segment = 300 cm²
h = Height of the spherical segment = 12 cm

R = ^A / _2πh
R = ³⁰⁰ / _{2 x π x 12}
That is, R = ³⁰⁰ / _75.41
R = 3.978

Therefore, the radius of the sphere is 3.978 cm.

Calculating the Height of the Spherical segment using the Surface Area of the Spherical Segment and the Radius of the sphere

h = ^A / _2πR

Where;
R = Radius of the sphere
A = Surface area of the spherical segment
h = Height of the spherical segment

Let’s solve an example;
Find the height of a spherical segment with a surface area of 420 cm² and a radius of 16 cm.

This implies that;
A = Surface area of the spherical segment = 300 cm²
R = Radius of the sphere = 16 cm

h = ^A / _2πR
h = ⁴²⁰ / _{2 x π x 16}
So, h = ⁴²⁰ / _100.544
h = 4.18

Therefore, the height of the spherical segment is 4.18 cm.

Read more: How to Calculate and Solve for the Volume of a Spherical Segment | Nickzom Calculator

How to Calculate the Surface Area of a Spherical Segment Using Nickzom Calculator

Nickzom Calculator – The Calculator Encyclopedia is capable of calculating the surface area of the spherical segment.

To get the answer and workings of the surface area of the spherical segment using the Nickzom Calculator – The Calculator Encyclopedia. First, you need to obtain the app.

You can get this app via any of these means:

Web – https://www.nickzom.org/calculator-plus

To get access to the professional version via web, you need to register and subscribe for NGN 1,500 per annum to have utter access to all functionalities.
You can also try the demo version via https://www.nickzom.org/calculator

Android (Paid) – https://play.google.com/store/apps/details?id=org.nickzom.nickzomcalculator
Android (Free) – https://play.google.com/store/apps/details?id=com.nickzom.nickzomcalculator
Apple (Paid) – https://itunes.apple.com/us/app/nickzom-calculator/id1331162702?mt=8

Once, you have obtained the calculator encyclopedia app, proceed to the Calculator Map, then click on Mensuration under the Mathematics section.

Now, click on Surface Area of the spherical segment under Mensuration

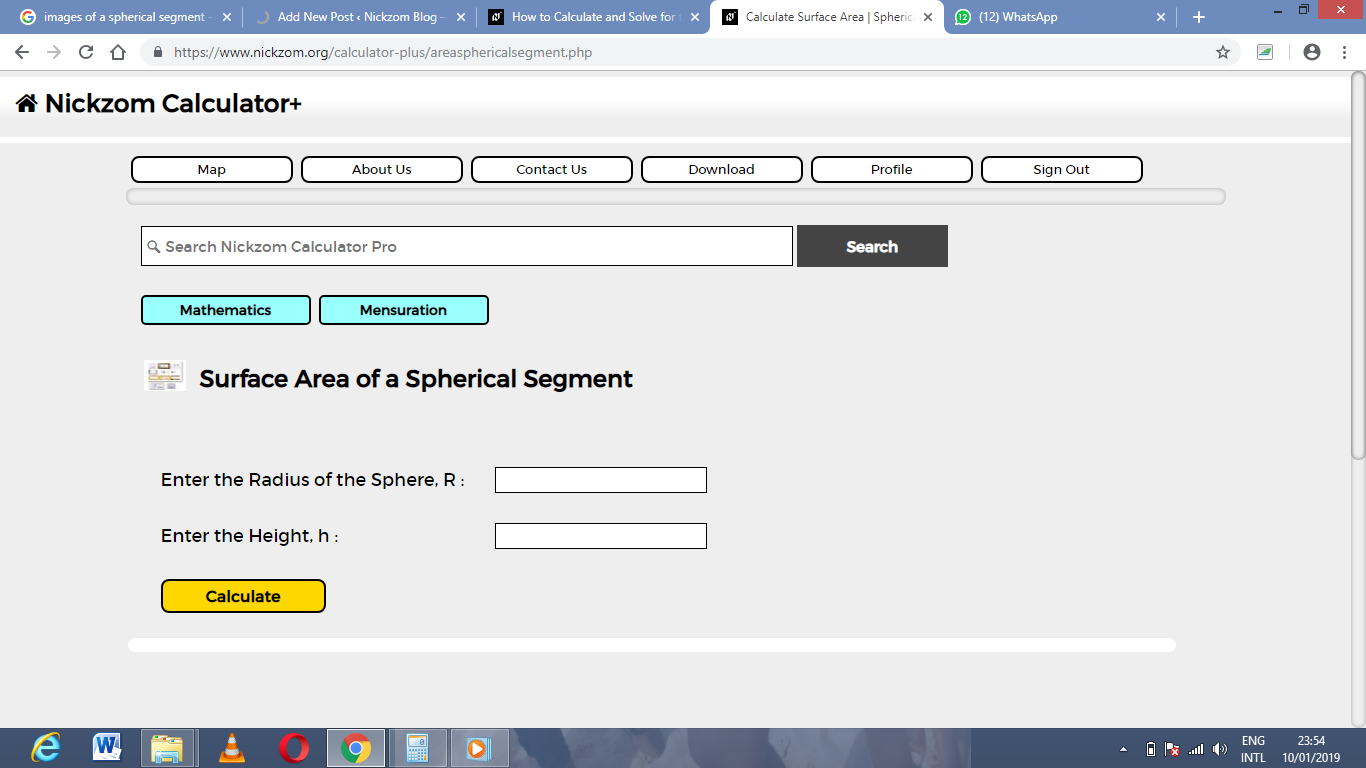
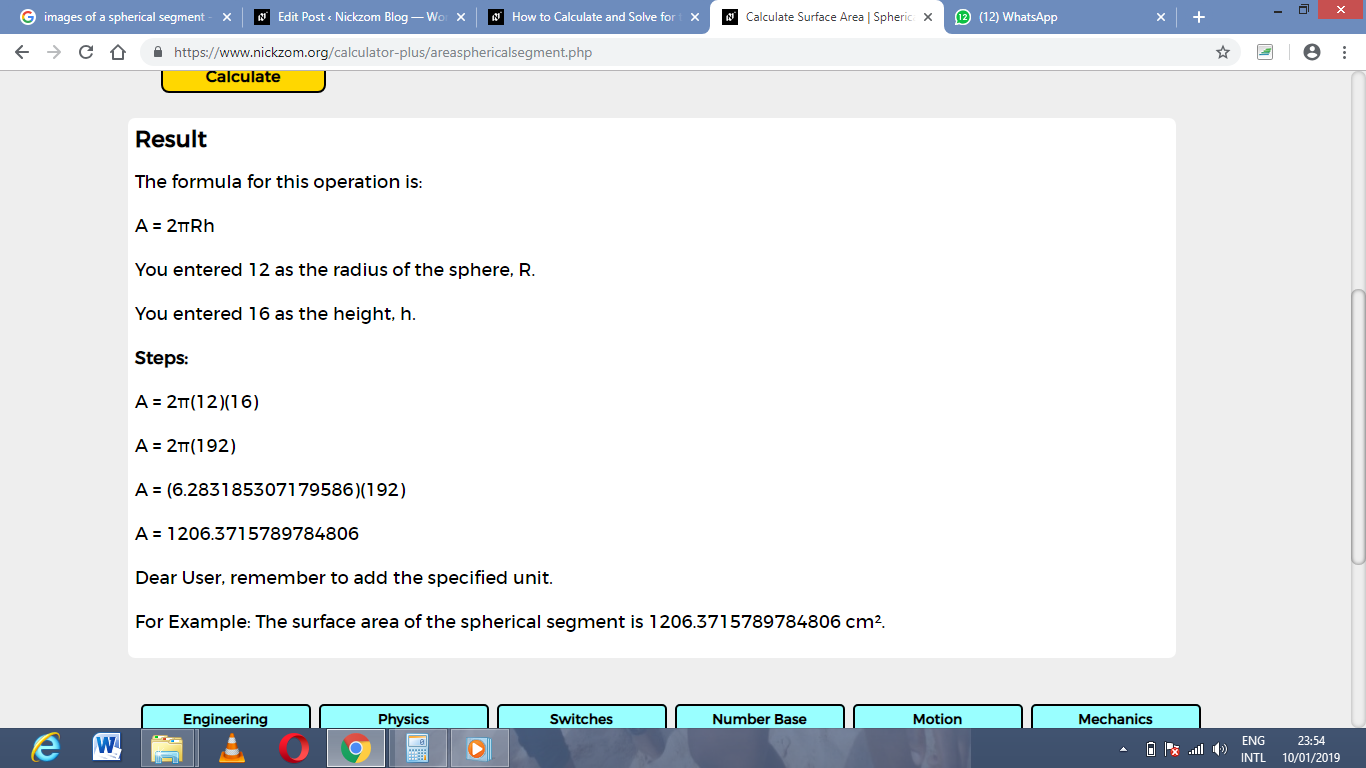
The screenshot below displays the page or activity to enter your values, to get the answer for the surface area of the spherical segment according to the respective parameters which are the radius of the sphere (R) and height (h).

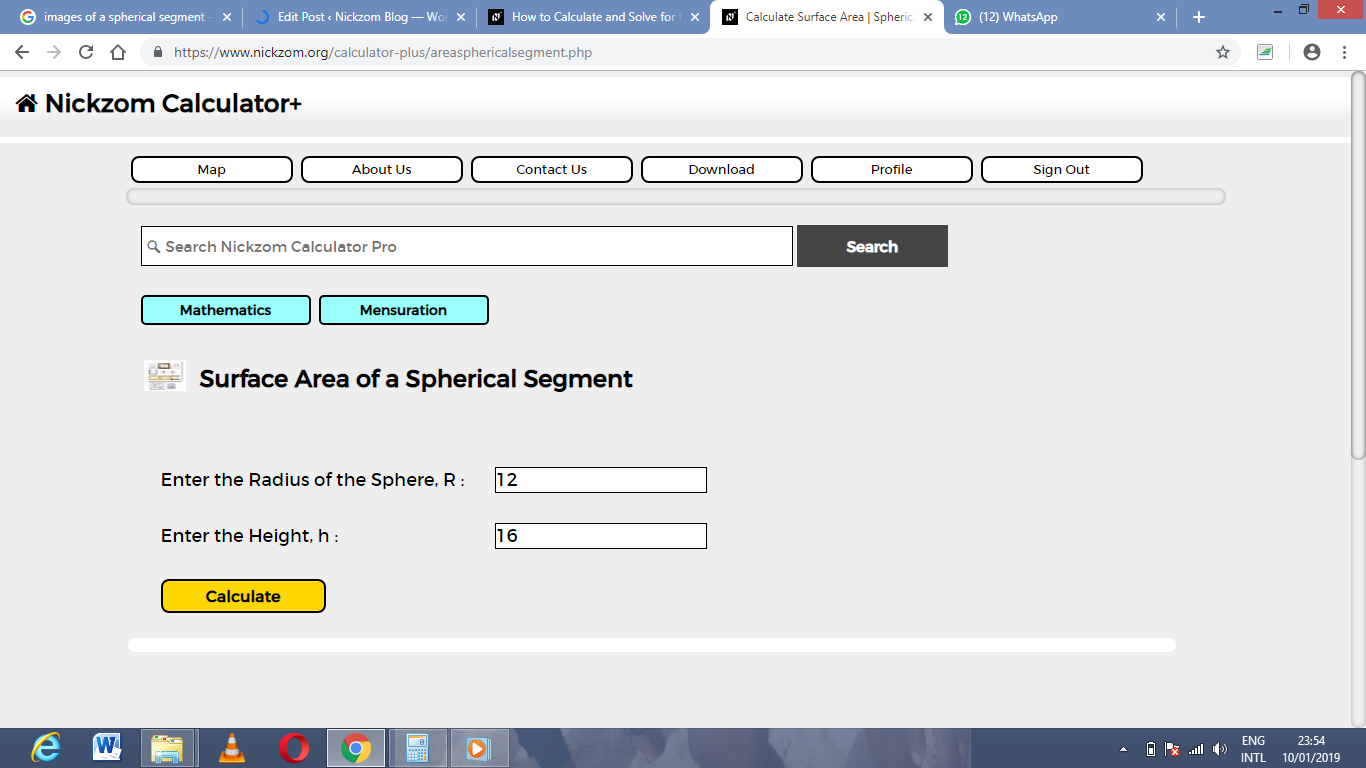
Now, enter the values appropriately and accordingly for the parameters as required by the example above where the radius of the sphere is 12 cm and the height is 16 cm.

Finally, Click on Calculate

As you can see from the screenshot above, Nickzom Calculator – The Calculator Encyclopedia solves for the Surface Area of a spherical segmentand presents the formula, workings and steps too.